Can ChatGPT help construct non-trivial statistical models? An in-depth exploration
Implementing complex statistical models in R can be a challenging task. However, with the assistance of ChatGPT, constructing non-trivial models becomes more accessible and efficient.

Exploring Bayesian Modeling in R with ChatGPT
Two years ago, a model for estimating treatment effects in a cluster-randomized stepped wedge trial was developed using a GAM with site-specific splines. Recently, there was an interest in exploring a Bayesian version of this model. ChatGPT was consulted for guidance on this endeavor.
ChatGPT confirmed the feasibility of building a model in R using Stan with cluster-specific random splines. This approach involves a hierarchical model where each cluster has its own spline, sharing a common structure.
Data Generation Process
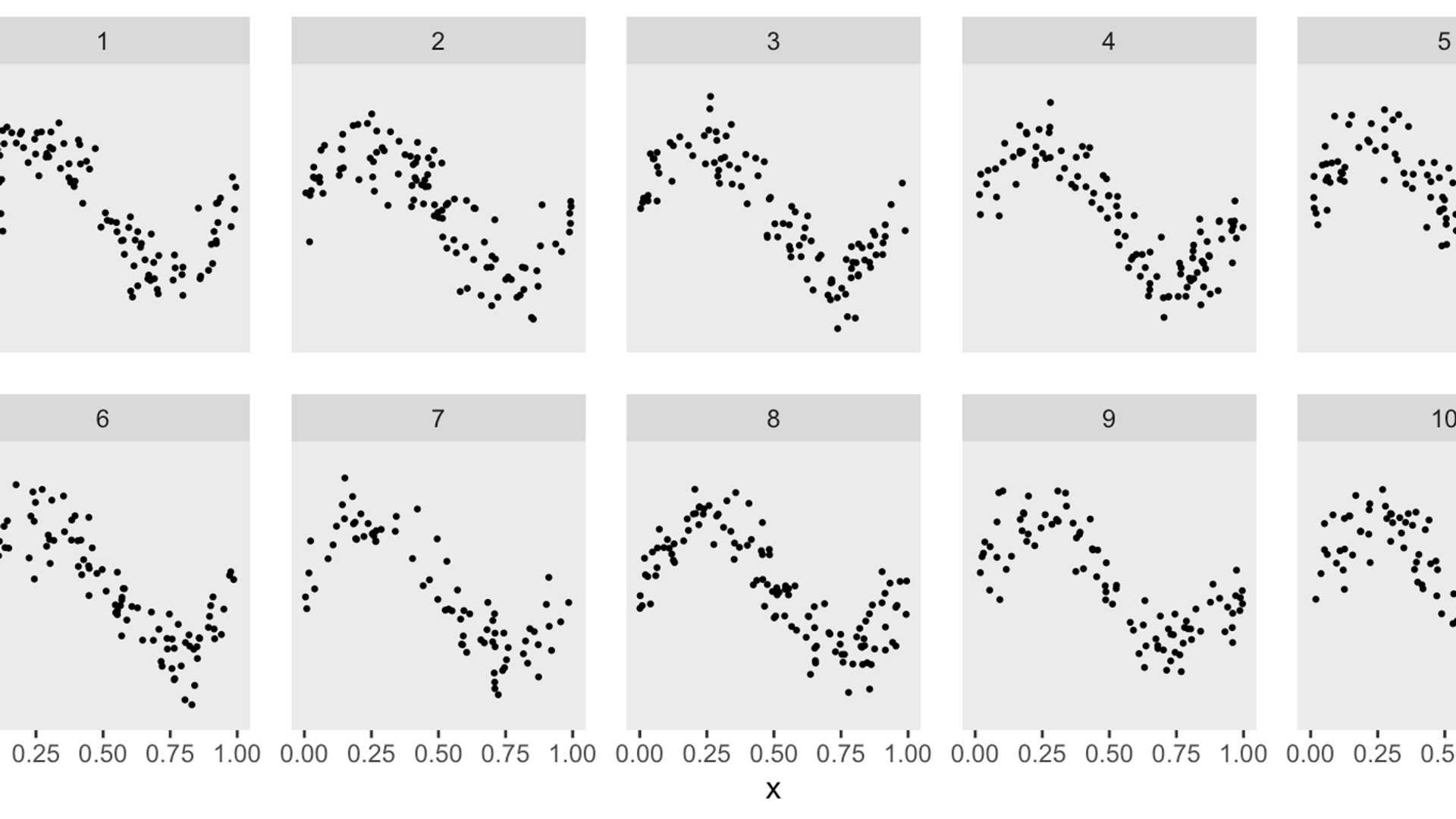
To explore different modeling options, a simple data generation process was required to create a simulated dataset. ChatGPT suggested using a non-linear function for \(y_{ik}\), the outcome for an individual \(i\) in cluster \(k\), based on the predictor \(x_{ik}\).
The initial code generated by ChatGPT had a limitation in creating cluster-specific spline curves. To address this, a cluster-specific effect \(a_k\) was introduced to stretch the sin curve differently for each cluster.
Modeling and Comparison
The aim was to estimate cluster-specific curves that capture the relationship between \(x\) and \(y\) within each cluster. The goal was to achieve a smooth and interpretable representation of the relationship while avoiding overfitting the data.

A GAM model was initially generated for comparison, providing insights into the relationship between \(x\) and \(y\). Subsequently, a Bayesian model was developed with a detailed description of data, parameters, likelihood, and priors.
Further, a penalized Bayesian spline model was created to enhance and smoothen the initial Bayesian model. By adding a penalization term based on the second derivative of the B-spline basis functions, the model achieved a more refined level of smoothing.
Comparing the penalized Bayesian model with the initial model showcased the significant impact of further smoothing, providing a more accurate representation of the underlying data trends.